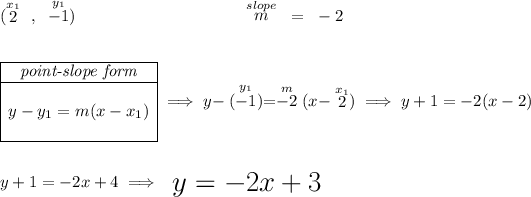keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the equation above
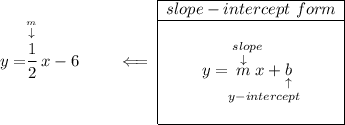
so for a perpendicular line to that one then
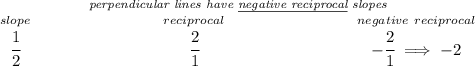
so we're really looking for the equation of a line whose slope is -2 and that it passes through (2 , -1)