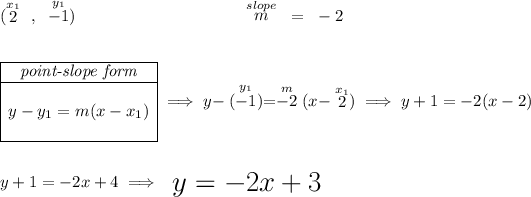Question

Write a slope intercept form to the equation of the line that is perpendicular to y= 1/2x-6

and passes through (2.-1)

Answer 1

keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the equation above

`y=\stackrel{\stackrel{m}{\downarrow }}{\cfrac{1}{2}}x-6\qquad \impliedby \begin{array}ll \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}`

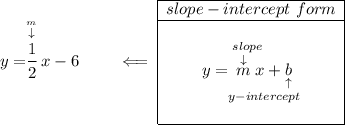
so for a perpendicular line to that one then

`\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{\cfrac{1}{2}} ~\hfill \stackrel{reciprocal}{\cfrac{2}{1}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{2}{1}\implies -2}}`

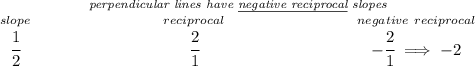
so we're really looking for the equation of a line whose slope is -2 and that it passes through (2 , -1)

`(\stackrel{x_1}{2}~,~\stackrel{y_1}{-1})\hspace{10em} \stackrel{slope}{m} ~=~ - 2 \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-1)}=\stackrel{m}{- 2}(x-\stackrel{x_1}{2}) \implies y +1= -2 (x -2) \\\\\\ y+1=-2x+4\implies {\LARGE \begin{array}{llll} y=-2x+3 \end{array}}`