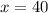Consider the figure posted below.
The cars start from the common point A. The car heading east travels a certain distance, say
 , and reaches point B. The car heading south travels 10 miles more, so
, and reaches point B. The car heading south travels 10 miles more, so
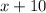 , and reaches point C. The distance between the two cars, BC, is 50.
, and reaches point C. The distance between the two cars, BC, is 50.
Since ABC is a right triangle, we can apply Pythagorean's theorem:
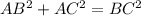
Plug the expressions/value for each side:
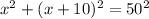
Expand/compute the squares:
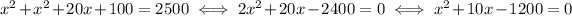
The two solutions of this equation are
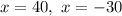
Since the cars can't travel a negative distance, the only acceptable solution is