Question

Which equations are correct

-6^4(4y^2+2)=-24y^8-12y^4

-4x^2(2x^2+5)=-8x^4-20x^2

-4b^3(5b^2+3)=-20b^6-12b^3

-5a^4(2a^2+4)=-10a^6-20a^4

Answer 1

2nd, 3rd and 4th equations are correct.

Explanation:

`-4x^2(2x^2+5)=-8x^4-20x^2\\\\`

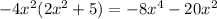
is right because each term inside is multiplied by -4x square and we find the answer is right.

`-4b^3(5b^2+3)\\\\\\= -4(5)(b^3)(b^2) =-20b^6-12b^3\\`

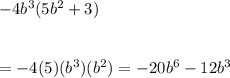
Hence correctly done.

`-5a^4(2a^2+4)=  (-5)(2)(a^4)(a^2)+(-5)(4)(a^4\\-10a^6-20a^4\\`

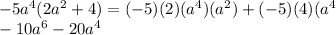
Correctly done.

`-6^4(4y^2+2)=-24y^8-12y^4\\= -(6)(6)(6)(6) 4y^2 -(6)(6)(6)(6) (2)`

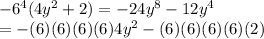
should be the right answer.

But instead only 6 is multiplied by inner terms. Hence wrong.

I answer is wrong and others are right.