Answer: The value of the expression is
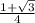 .
.
Step-by-step explanation:
The given expression is,
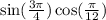
Step 1: Break the angles.
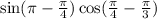
Step 2: Use quadrant concept to find the value of
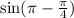
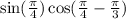
Step 3:Use
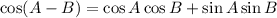
![\sin ((\pi)/(4))[\cos ((\pi)/(4))\cos ((\pi)/(3))+\sin ((\pi)/(4))\sin ((\pi)/(3))]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/546v5moogrt85fijb2lclry2a1loeravpb.png)
Step 4: Put these values by using trigonometric table.
![((1)/(\sqrt 2))[((1)/(\sqrt 2))((1)/(2))+((1)/(\sqrt 2))((\sqrt3)/(2))]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/dh3ect02jzuxbe9c4ie0gh321c25vcnxtk.png)
![((1)/(\sqrt 2))[((1)/(2\sqrt 2))+((\sqrt3)/(2\sqrt 2))]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/jzg50t0ehyrdslyn6a14twat2s772p64w6.png)
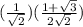
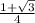
Therefore, the value of the expression is
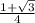 .
.