Question

In the right triangle shown, ∠a=30° and ab = 12√3 how long is ac

Answer 1

Given that in the right triangle , ∠A=30° and AB = 12√3 .

As the figure is missing and its not clearly mentioned that AB is the base or hypotenuse of the right triangle. So two cases arises-

Case 1: AB is the base for ∠A of the right triangle (as shown in figure 1).

As we know from the trigonometric ratio that,
`cos(\theta) = (base)/(hypotenuse)`

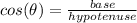
Here , AB is the base and AC is the hypotenuse , and ∠A=30°

`\Rightarrow cos(30)=(AB)/(AC) \\\\\Rightarrow AC=(AB)/(cos(30))`

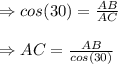
The value of
`cos(30)=(√(3) )/(2)`

`\Rightarrow AC=12√(3)*(2 )/(√(3) )\\\\\Rightarrow AC=24`

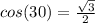
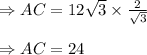
Hence, AC is 24 unit long.

Case 2: AB is the hypotenuse for ∠A of the right triangle (as shown in figure 2).

As we know from the trigonometric ratio that,
`cos(\theta) = (base)/(hypotenuse)`

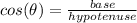
Here , AB is the hypotenuse and AC is the base, and ∠A=30°

`\Rightarrow cos(30)=(AC)/(AB) \\\\\Rightarrow AC=AB*cos(30)`

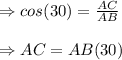
The value of
`cos(30)=(√(3) )/(2)`

`\Rightarrow AC=12√(3)*(√(3))/(2)\\\\\Rightarrow AC=18`

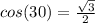
Hence, AC is 18 unit long.