Answer 1:
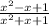
Here given that, x is real that is the domain
Range of the given expression is :
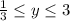
Write it interval form.
![[(1)/(3),3]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/s4l3mywzrvykss53xvvqobvtn5kaz6l30l.png) Option (2)
Option (2)
Answer 3:
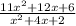
Here domain is all real x.
Range is :
{y ∈ R : y ≤ -5 or y ≥ 3}
In interval form:
(-∞, -5] ∪ [3, ∞)
So, y can't lies between -5 to 3 Option (2)
Answer 5 :
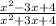
Here domain is :
x is real
And range is :
{y ∈ R :
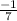 ≤ y ≤ 7}
≤ y ≤ 7}
We see that maximum y value is 7.
So, maximum value is 7. Option (4)
Answer 6:

Solve for x .
Square both the side
9x² + 6x + 1 = 4 + x² - 4x
8x² + 10x - 3 < 0
(2x + 3)(4x - 1) < 0
2x + 3 = 0 & 4x - 1 = 0
x =
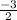 & x =
& x =

So,
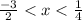
x ∈
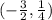 Option (1)
Option (1)