Question

We take a milk carton from the refrigerator and put it on the table at room temperature. We assume that the temperature of the carton, T, as a function of time follows Newton's cooling law:

dT / dt = k (T - a),
where a is the temperature of the surroundings and k is a constant. We assume the temperature
the surroundings are a = 20 (given in ◦C), and that T (0) = 4 (given in ◦C).
a) Show that T (t) = 20 - 16e ^ kt (given in ◦C).
b) After 5 minutes the temperature of the carton is 8◦C. What is the temperature after 15 minutes?

Answer 1

We can solve this problem using separation of variables.

Then apply the initial conditions

Step-by-step explanation

We were given the first order differential equation


`(dT)/(dt)=k(T-a)`

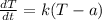
We now separate the time and the temperature variables as follows,


`(dT)/(T-a)=kdt`

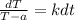
Integrating both sides of the differential equation, we obtain;


`ln(T-a)=kt +c`

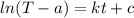
This natural logarithmic equation can be rewritten as;


`T-a=e^(kt +c)`

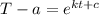
Applying the laws of exponents, we obtain,


`T-a=e^(kt)* e^(c)`


`T-a=e^(c)e^(kt)`

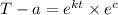
We were given the initial conditions,


`T(0)=4`

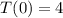
Let us apply this condition to obtain;


`4-20=e^(c)e^(k(0))`


`-16=e^(c)`

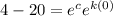
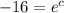
Now our equation, becomes


`T-a=-16e^(kt)`

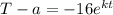
or


`T=a-16e^(kt)`

When we substitute a=20,
we obtain,


`T=20-16e^(kt)`

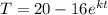
b) We were also given that,


`T(5)=8`

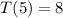
Let us apply this condition again to find k.


`8=20-16e^(5k)`

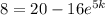
This implied


`-12=-16e^(5k)`


`(-12)/(-16)=e^(5k)`


`(3)/(4)=e^(5k)`

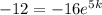
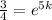
We take logarithm to base e of both sides,


`ln((3)/(4))=5k`

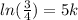
This implies that,


`(ln((3)/(4)))/(5)=k`



`k=-0.2877`

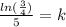
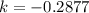
After 15 minutes, the temperature will be,



`T=20-16e^(-0.2877* 15)`


`T=20-0.21376`



`T=19.786`

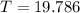
After 15 minutes, the temperature is approximately 20°C