Answer:
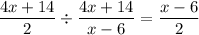
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Dividing Fractions - KCF (Keep Change Flip)
- Keep the 1st fraction the same
- Change the sign from division to multiplication
- Flip the 2nd fraction (reciprocate)
Algebra I
- Terms/Coefficients
- Domains
Explanation:
Step 1: Define
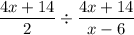
Step 2: Simplify
- Divide [KCF]:
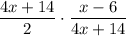
- Multiply:

- Divide:
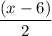
Extra:
If we were to graph this, we would need to watch out for domain restrictions or changes because we are combining 2 domains together when 1 of them has a restriction.