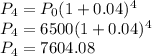Answer:
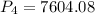
Explanation:
If the population increases at a rate of 4% per annum, then:
In year 1:
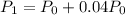
Where
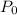 is the initial population and
is the initial population and
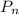 is the population in year n
is the population in year n
In year 2
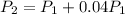
It can also be written as:
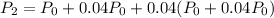
Taking out common factor
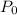
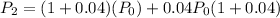
Taking out common factor (1 + 0.04)
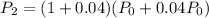
Taking out again common factor
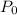
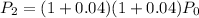
Simplifying
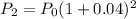
So
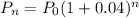
This is the equation that represents the population for year n
Then, in 4 years, the population will be: