Question

5) (3 parts) Calculate the average density of the following objects (assume they are all perfect spheres). Use the steps detailed in the examples.

SHOW ALL YOUR WORK (formulas used, numbers plugged in with proper UNITS, and clearly indicate final answer!

a) Mass=6.0x1024kg, Diameter=12000km (12,000,000 meters)

b) Mass=2.0x1030kg, Diameter=1.4x106km

c) What objects in our Solar System are similar to the objects in part a and b in terms of size and density (see appendix tables)? Which one has greater average density?

6) (2 parts) Suppose you have a moon of mass of 4.8x1022kg, and a diameter of 3100km (3,100,000m).

a) Calculate the average density of this moon.

b) Considering that water ice has a density of around 1000kg/m3, and silicate rock is around 3000kg/m3, is the bulk of this satellite mostly ice or rock?

PLEASE SHOW ALL STEPS!!!

Answer 1

5 a) Mass = 6.0 × 10²⁴ kg; d = 12 × 10⁶ m

`r  = (1)/(2)d = (1)/(2) * 12 *10^(6)\text{ m} = 6.0 * 10^(6) \text{ m}\\`

`V = (4)/(3) \pi r^(3) = (4)/(3) \pi * (6.0 * 10^(6) \text{ m})^(3) = 9.05 * 10^(20) \text{ m}^(3)\\`

`\text{Density} = \frac{\text{Mass}}{\text{Volume}} = \frac{6.0 * 10^(24)\text{ kg}}{9.05 * 10^(20) \text{ m}^(3)} = \text{6600 kg/m}^(3)\\`

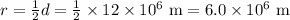
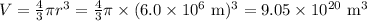
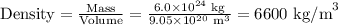
The average density is 6600 kg/m³.

5 b) Mass = 2.0 × 10³⁰ kg; Diameter = 1.4 × 10⁶ km

`r  = (1)/(2)d = (1)/(2) * 1.4 *10^(9)\text{ m} = 7.0 * 10^(8) \text{ m}\\`

`V = (4)/(3) \pi r^(3) = (4)/(3) \pi * (7.0 * 10^(8) \text{ m})^(3) = 1.43 * 10^(27) \text{ m}^(3)\\`

`\text{Density} = \frac{\text{Mass}}{\text{Volume}} = \frac{2.0 * 10^(30)\text{ kg}}{1.43 * 10^(27) \text{ m}^(3)} = \text{1400 kg/m}^(3)\\`

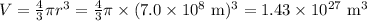
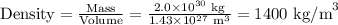
The average density is 1400 kg/m³.

5 c) Venus and the Sun are most like the objects in Parts a) and b). Venus has the greater density

6 a) Mass = 4.8 × 10²² km; Diameter = 3.1 × 10⁶ m

`r  = (1)/(2)d = (1)/(2) * 3.1 *10^(6)\text{ m} = 1.55 * 10^(6) \text{ m}\\`

`V = (4)/(3) \pi r^(3) = (4)/(3) \pi * (1.55 * 10^(6) \text{ m})^(3) = 1.56 * 10^(19) \text{ m}^(3)\\`

`\text{Density} = \frac{\text{Mass}}{\text{Volume}} = \frac{4.8 * 10^(22)\text{ kg}}{1.56 * 10^(19) \text{ m}^(3)} = \text{3100 kg/m}^(3)\\`

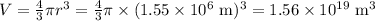
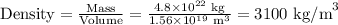
The average density of the moon is 3100 kg/m³.

6 b) The satellite appears to consist mostly of silicate rock.