Question

What is the solution to the system of equations below?

2x-y=10 and y=-1/2x+5

(6, 2)
(6, –2)
(–6, –22)
(–6, 8)

Answer 1

The correct answer is:

(x,y) = (6,2)

Option A would be the correct one.

Answer 2

The answer is (6, 2).

Explanation:

This is a system of equations so we have to replace one equation in the other one, this is:

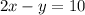`2x-y=10` Eq. 1

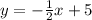`y=-(1)/(2)x+5` Eq. 2

Replacing the Eq. 2 in the Eq. 1, we have:

`2x-(-(1)/(2)x+5)=10`

`2x+(1)/(2)x-5=10`

`2.5x=10+5`

`x=(15)/(2.5)`

`x=6`

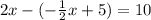
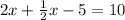
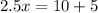
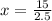
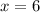
Now we have that x=6, we can replace it in the Eq. 2:

`y=-(1)/(2) *6+5\\y=-3+5\\y=2`

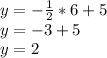
Now y=2

From the above we have that the answer is (6, 2) expressed in Cartesian coordinates.