We were given;
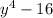
to factor over the complex numbers.
We can rewrite the given expression to look like difference of two squares,
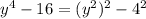
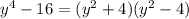
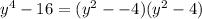
We can still rewrite as,

We can still rewrite as
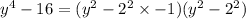
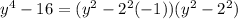
Applying difference of two squares again, we have;
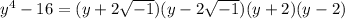
Note that, in complex numbers

