Answer:
focus is (1,0)
Explanation:
the focus of a parabola with equation

Focus point lies inside the parabola
To find the focus of a parabola we need to find the vertex
the distance between the focus and vertex is the value of p.
Focus point is (h+p,k)
Where (h,k) is the vertex
Given equation is in the form of
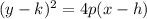
Given equation can be written as
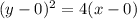
So the vertex is (0,0)
Now we find the value of p
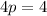
So
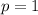
Focus is (h+p,k) that is (1,0)