Question

Jeremy is recording the weights, in ounces, of different rock samples in a lab. The weights of seven rocks are listed below.

11, 13, 14, 6, 10, 9, 10

The eighth rock that he weighed was 5 ounces. How would the interquartile range of the data be affected if Jeremy includes the weight of the eighth rock?

Jeremy is recording the weights, in ounces, of different rock samples in a lab. The weights of seven rocks are listed below.

11, 13, 14, 6, 10, 9, 10

The eighth rock that he weighed was 5 ounces. How would the interquartile range of the data be affected if Jeremy includes the weight of the eighth rock?

Answer 1

The value of the (RIC) will increase from 4 to 5.75, that is, 44%

Explanation:

To answer this question you have to know the definition of Rank well.

The range is defined as the difference between the maximum and minimum value of a series of data. Xmax - Xmin

The interleaving range (RIC) is a measure of dispersion that measures the central range of 50% of the data.

Therefore, if a low value is included, such as five, the variance of the data would be greater and, consequently, the value of the (RIC) will increase from 4 to 5.75, that is, 44%

Answer 2

Hence the interquartile range increased by 3(7-4) when we included the eight weight.

Explanation:

The weight of the seven rocks is given as:

11 13 14 6 10 9 10

on arranging the data in the ascending order we get the observation as:

6 9 10 10 11 13 14

we divide our data into 3 sets:

the median of data(
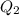`Q_2`) is: 10 (as it is the middle value among the data)

The lower set of data is:

6 9 10

`Q_1=9` ( as it is the middle value)

The upper set of data is:

11 13 14

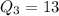`Q_3=13` ( as it is the middle value in the upper set of data)

Hence, the interquartile range is:
`Q_3-Q_1=13-9=4`

The weight of eight rocks is given as:

11 13 14 6 10 9 10 5

On arranging the data in ascending order we get:

5 6 9 10 10 11 13 14

The median of the data is denoted by
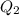`Q_2` which is the middle value of the given data.

Hence the median here is between 10, 10.

so, the median is given by:

`(10+10)/(2)=10`

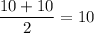
thus
`Q_2=10`

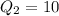
also the lower set of data is:

5 6 9

Thus
`Q_1=6` (as it is the middle value in the lower set of data)

the upper set of data is:

11 13 14

Thus
`Q_3=13`

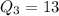
Hence, the interquartile range is:

`Q_3-Q_1=13-6=7`

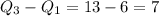
So when we were having seven weights the interquartile range was: 4

and when we included the eight weight the interquartile range becomes: 7

Hence the interquartile range increased by 3(7-4) when we included the eight weight.