Answer: The point A is 26m above from the ground.
Step-by-step explanation:
It is given that the maximum drop Is 65m over a horizontal distance of 65m in two sections. So, the maximum value is (65,65) and the value is (0,0) when it stops.
From the given information it is noticed that the first section has a gradient of 3 and the second section has a gradient of 1/2.
The equation of line passing through the point
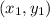 with slope m is define as,
with slope m is define as,

For first section the slope is 3 and the point is (65,65).
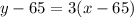
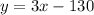 ..... (1)
..... (1)
For second section the slope is 1/2 and the point is (0,0).
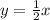 .....(2)
.....(2)
Put
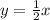 in equation (1), we get,
in equation (1), we get,
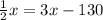

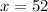
Put this value in equation (2)
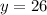
Therefore, the point A is 26m above the ground and the horizontal distance is 52m from the endpoint.