Question

Alpha Inc. produces 500 units of a product. The selling price of each unit is $4. The company decides sells 100 additional units. Now, the total revenue earned from selling all the units is $3,000. What is the marginal revenue?

Answer 1

Marginal Revenue is the revenue realised by selling additional units of a product.

Mathematically, Marginal Revenue can be expressed as,

`MR =(Change\:in\: Total\:Revenue)/(Change\:in\:Quantity)`

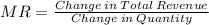
Let old Quantity be
`Q_1` and new Quantity be
`Q_2`

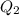
Since 500 units were produced first,

`Q_1=500`

And now 100 additional units will be produced, So

`Q_2=500+100=600`

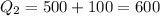
Now Change in Quantity produced is

`Q_2-Q1=600-500=100`

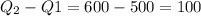
Now we need to calculate for the Change in Total Revenue

We also let the initial total revenue be

`TR_1`.

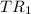Initially 500 units were sold for $4 per unit. This implies that,

`TR_1=4*500`.

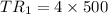=$2,000

We were given the current total revenue to be $3,000.

This implies that, our change in total revenue

`TR_2- TR_1=3,000-2,000=1,000`.

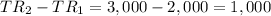Hence our Marginal Revenue

`MR =\frac{1,000} {100}`

`MR =10`

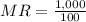
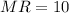
Hence the Marginal Revenue is $10.