Question

The one-time fling! Have you ever purchased an article of clothing (dress, sports jacket, etc.), worn the item once to a party, and then returned the purchase? This is called a one-time fling. About 20% of all adults deliberately do a one-time fling and feel no guilt about it! In a group of nine adult friends, what is the probability of the following?

Answer 1

Given that about 20% of adults do one time fling.

That is probability of a person doing fling is
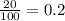`(20)/(100)=0.2` . Let it be p.

Then we have to use binomial distribution formula for the given problems.

b(x;n,p)=
`n_{C_(x)}p^(x)(1-p)^(n-x)`

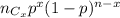
A)Probability of no one has done one time fling means x is 0 here.

Hence
`b(0;9,0.2)=9_{C_(0) }(0.2)^(0)(1-0.2)^(9)`

`=1X1X0.8^(9)=0.1342`

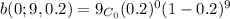
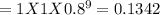
b) Probability of at least one person has done fling=1-(probability of no one has done)

=1-0.1342=0.8658

c)Probability of no more than two people have done one time fling means we need to add the probabilities for x=1,x=2 along with x=0.

`b(1;9,0.2)=9_{C_(1)}(0.2)^(1)(1-0.2)^(8)`

`=9X0.2X0.8^(8)=0.302`

`b(2;9,0.2)=9_{C_(2)}0.2^(2)(1-0.2)^(7)`

`=36X0.04X0.8^(7)=0.302`

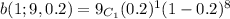
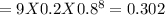
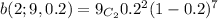
Hence probability = 0.1342+0.302+0.302 = 0.7382