Question

Now, suppose one of the roots of the polynomial function is irrational. The roots of the function are 2,
`√(3)`, and 5. Write the equation for this polynomial function.

Which of the following must also be a root of the function?
-
`√(3)`

The equation of the polynomial function is:
f(x)=(x-2)(x-5)(x-
`√(3)`)(x+
`√(3)`)

EXPAND:

f(x) = 
`x^(4)`- _________
`x^(3)`+_________
`x^(2)`+_________x-__________

Answer 1

b. -√3

hope this helps! :o)

Answer 2

1. Since, the roots of the function are 2,
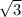`√(3)` and 5. We have to write the equation for this polynomial function.

So, the equation is
`(x-2)(x-\sqrt3)(x-5)=0`.

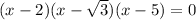2. Now, the equation of the polynomial function is

`f(x) = (x-2)(x-5)(x-\sqrt3)(x+\sqrt3)`

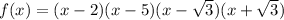
We have to find its expanded form.

we will proceed from step by step to find the expanded form.

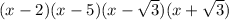
`(x-2)(x-5)(x-\sqrt3)(x+\sqrt3)`

=
`[(x-2)(x-5)][(x-\sqrt3)(x+\sqrt3)]`

=
`[x^2-7x+10][x^2-3]`

=
`(x^4-7x^3+10x^2-3x^2+21x-30)`

=
`x^4-7x^3+7x^2+21x-30`

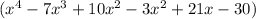
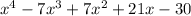
So, the expanded form of the given polynomial function is:

f(x) = =
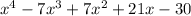`x^4-7x^3+7x^2+21x-30`.