For this case we have:
We define the following variable
x : Speed of the car in South direction
By definition, we know that:
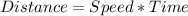
For the car in north direction:

For the car in south direction:
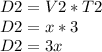
The distance between both cars, after 3 hours, is:
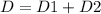
So, we have:
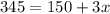
Clearing x;
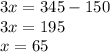
Thus, the speed of the car in the south direction is
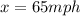
Answer:
Option B