Question

Find the tangent line(s) to the parabola y = (x-1)^2 that has a slope of 10.

Answer 1

Ex 1

The slope of the tangent line is given by the derivative of the function, so you have

`f(x) = (x-1)^2 \implies f'(x) = 2(x-1)`

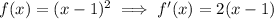
So, if you want the slope to be 10, you have

`2(x-1) = 10 \iff x-1 = 5 \iff x = 6`

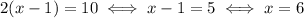
The point on the graph for x=6 is

`(6,f(6)) = (6, 2(6-1)^2) = (6, 50)`

So, we want a line passing through this point with slope 10. You can use the formula

`y-y_0=m(x-x_0)`

to get

`y-50=10(x-6) \iff y = 10x-60+50 \iff y = 10x-10`

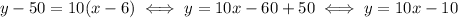
Ex 2

The cirlce
`x^2+y^2=1` has center 0 and radius 1. So, a tanget line passing through (0,-3) will touch the lower half of the circle, which can be expressed as

`y = -√(1-x^2)`

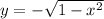
All lines passing through (0,-3) have equation like
`y=mx-3`

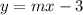
So, if we put these two equation in a system, we have

`\begin{cases} y= -√(1-x^2)\\y=mx-3\end{cases}`

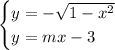
Since the left hand sides are the same, the right hand sides must be the same as well:

`-√(1-x^2)=mx-3`

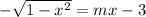
Squaring both sides, you get to the following quadratic equation:

`1 - x^2 = m^2 x^2 - 6 m x + 9`

whose discriminant is
`m^2-8`

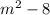
We want this system to have one solution, so that the line and circle meet in one point, and thus the line is tangent to the circle. This happens if the discriminant equals zero, i.e.

`m^2-8=0 \iff m = \pm√(8) = \pm2√(2)`

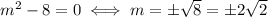
So, the two tangent lines are

[tex ] y = \pm2\sqrt{2}x-3 [/tex]

You can plot the circle and the lines on a graphic calculator to see that this is the correct solution