Answer:
Amount invested at 7% = 16000
Amount invested at 9% = 12000
Explanation:
Let x be the amount invested at 7% and y be the amount invested at 9%.
Since the total amount invested is $28000, therefore, we can set up the first equation as:

Secondly, we are give that sum of two investments is $2200. Therefore, we can write the second equation as:
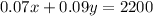
Now we need to solve these two equations to get the values of x and y.
First of all, we multiply the second equation with 100 in order to get rid of decimal values.

Let us use substitution method here. First of all we will solve for y from first equation and plug that into second equation.
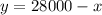
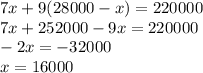
Therefore, amount invested at 7% is $16000 and amount invested at 9% is 28000-16000=$12000.