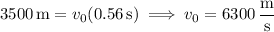4. The Coyote has an initial position vector of
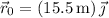 .
.
4a. The Coyote has an initial velocity vector of
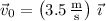 . His position at time
. His position at time
 is given by the vector
is given by the vector
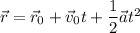
where
 is the Coyote's acceleration vector at time
is the Coyote's acceleration vector at time
 . He experiences acceleration only in the downward direction because of gravity, and in particular
. He experiences acceleration only in the downward direction because of gravity, and in particular
 where
where
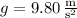 . Splitting up the position vector into components, we have
. Splitting up the position vector into components, we have
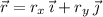 with
with
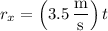
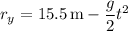
The Coyote hits the ground when
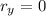 :
:

4b. Here we evaluate
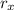 at the time found in (4a).
at the time found in (4a).
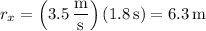
5. The shell has initial position vector
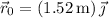 , and we're told that after some time the bullet (now separated from the shell) has a position of
, and we're told that after some time the bullet (now separated from the shell) has a position of
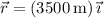 .
.
5a. The vertical component of the shell's position vector is
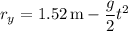
We find the shell hits the ground at
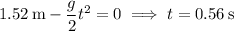
5b. The horizontal component of the bullet's position vector is
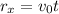
where
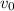 is the muzzle velocity of the bullet. It traveled 3500 m in the time it took the shell to fall to the ground, so we can solve for
is the muzzle velocity of the bullet. It traveled 3500 m in the time it took the shell to fall to the ground, so we can solve for
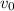 :
: