Question

Step by step explanation please :-D

Solve the equation. Check for extraneous solutions.

9|9 – 8x| = 2x + 3

Answer 1

To solve an absolute value equation of the form |X| = k, where X is an expression with a variable and k is a non-negative number or an expression, you must solve the compound equation X = k or X = -k.

The first step is to divide both sides by 9 to get the absolute value of an expression equal to a non-negative number.

9|9 – 8x| = 2x + 3

Divide both sides by 9.

`|9 - 8x| = (2x + 3)/(9)`

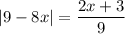
Now we eliminate the absolute value by rewriting this as a compound equation.

`9 - 8x = (2x + 3)/(9) ~~~or~~~ 9 - 8x = -(2x + 3)/(9)`

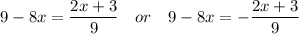
We must solve both equations.

Multiply both sides by 9.

`9(9 - 8x) = 2x + 3 ~~~or~~~ 9(9 - 8x) = -(2x + 3)`

`81 - 72x = 2x + 3 ~~~or~~~ 81 - 72x = -2x - 3`

`-74x = -78 ~~~or~~~ -70x = -84`

`x = (-78)/(-74) ~~~or~~~ x = (-84)/(-70)`

`x = (39)/(37) ~~~or~~~ x = (6)/(5)`

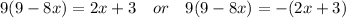
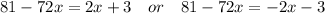
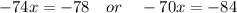
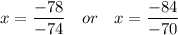
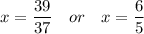
Answer: x = 39/37 or x = 6/5

To check for extraneous solutions, we plug in each solution into the original equation and check if it works.

Check 39/37:

9|9 – 8(39/37)| = 2(39/37) + 3

|81 - 72(39/37)| = 78/37 + 3

|2997/37 - 2808/37| = 78/37 + 111/37

|189/37| = 189/37

189/37 = 189/37

The solution 39/37 is valid.

Check x = 6/5.

9|9 – 8x| = 2x + 3

9|9 – 8(6/5)| = 2(6/5) + 3

|81 - 72(6/5)| = 12/5 + 15/5

|405/5 - 432/5| = 27/5

|-27/5| = 27/5

27/5 = 27/5

The solution x = 6/5 is also valid.

There are no extraneous solutions.