Question

How many congruent triangles do the midsegments of an equilateral triangle partition the triangle into? Explain.

Answer 1

4

Explanation:

Let us consider an equilateral triangle ABC. Now, we will define midsegments:

A midsegment of a triangle is a segment that connects the midpoints of two sides of a triangle (here triangle ABC). This segment has two special properties. It is always parallel to the third side, and the length of the midsegment is half the length of the third side.

Refer the attached image:

Now, from the definition of midsegment we can see that:

`PQ=(1)/(2)BC`

`\therefore PQ=BR`

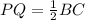
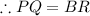
and PQ is also parallel to BR.

Now, again from the definition of midsegment we can see that:

`QR=(1)/(2)AB`

`\therefore QR=PB`

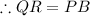
and QR is parallel to PB.

therefore, PQBR forms a parallelogram

And a diagonal of a parallelogram divides it into two congruent triangles.

Hence, triangle 2 (triangle PBR) is congruent to triangle 4(triangle PQR).

Similarly, triangle 3 (triangle QRC) and triangle 1 (triangle APQ) are congruent to triangle 4 (triangle PQR), Therefore, there are 4 congruent triangles formed when midsegments of an equilateral triangle partition the triangle.