Question

The weekly salaries (in dollars) for

9

employees of a small business are given below.
(Note that these are already ordered from least to greatest.)

679, 715, 799, 844, 891, 917, 938, 1002, 1027 Suppose that the
$
1027

salary changes to
$
946

. Answer the following.


(a) What happens to the median?

It decreases by




$
.


It increases by




$
.


It stays the same.


(b) What happens to the mean?

It decreases by




$
.
9


It increases by




$
.


It stays the same.

Answer 1

a) Median stays the same

b) Mean is decreased by $9

Explanation:

The median is the number or the average of the two numbers that is in the middle of a sorted distribution of numbers,

Here the median number will be the 5th number counting from left or right from the sorted list of numbers. Therefor is is 891.

When 1027 is changed to 946 it will fall between 938 and 1002. So updated sorted list of numbers will now look like,

679, 715, 799, 844, 891, 917, 938, 946, 1002

Here also median will be the 5th number which will be equal to 891.

Therefore, , median will not change.

Mean is the value we get by taking the total value of the salaries and divide it by the number of employees.

In the initial case,

Mean =
`(679+715+799+844+891+917+938+1002+1027)/(9) =868`

When the salary is changed from $1027 to $946,

Mean=
`(679+715+799+844+891+917+938+1002+946)/(9) =859`

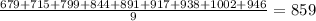
Therefor we can see that Mean has decreased by $9.