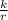Answer:
To find the sum of a + b where a and b are rational number.
1. when a and b are natural numbers
just add them . for example a =3, b=8
then ,a + b = 11
2. When a and b are whole numbers,
simply add them . for example a= 0, b=8
a+ b = 0 + 8= 8
3. When a and b are integers
for example, a =-1 b=8,
a+ b= -1+ 8 =7,
a=-2, b= -8
a+ b= -2-8=-10
a= -6 , b=2
a+ b= -6 + 2= -4
a= 8, b= -2
a+ b= 8 +(-2) =6
I have written this because Rational number = [Integers{Whole number(Natural number)}]
now when a= Any fraction=
 and b = Any fraction=
and b = Any fraction=
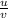
now ,
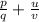
Find L.C.M of q and v
= if q and v are Co-prime , just multiply them to find their L.C.M.
For example 14,9. LCM=14×9=126
Otherwise, Find factors of q and v . Then take out common factors first and then multiply the remaining with with common factors.For example
q=12 and v=18
12 =2×2×3
18=2×3×3
common factor =2,3
non common=2,3
L.C.M= 2×2×3×3=36
Suppose LCM of q and v = r
then ,
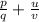
=
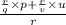
=
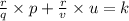
then ,
a + b=