Question

If a and b are integers such that a2 − b2 = 100, what is the greatest possible value of a?

Answer 1

26

Explanation:

Question says that 'a' and 'b' are integers that implies we cannot have 'a' and 'b' in the form of decimals.

Now, lets expand the given equation:

`a^2-b^2=100`

`(a+b)(a-b)=100`

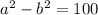
Lets say:
`(a+b)=p`,
`(a-b)=q`

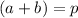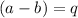
Let us consider the factor pairs of 100.

`(1 * 100), (2 * 50), (4 * 25), (5 * 20), (10 * 10), (20 * 5), (25 * 4), (50 * 2), (100 * 1)`

Only factor pair
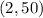`(2,50)` gives us the integer values of 'a' and 'b'.

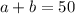`a+b=50`....equation (1)

`a-b=2`........ equation (2)

adding equation 1 and 2, we get:

`2a=52`

`a=(52)/(2)=26`

`a-b=2`

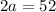
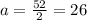
Plugging the value of 'a' in the equation 2

`26-b=2`

`b=24`

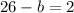
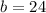
So the greatest possible value of 'a' is 26.