Question

A kangaroo is capable of jumping to a height of 2.62 m. determine the takeoff speed of the kangaroo.

a) 717
b) 8.2
c) 5.92
d) 7.17

Answer 1

vi = 7.17 m/s

Step-by-step explanation:

(4225 m2/s2)/(6 m/s2) = d

d = 704 m

Return to Problem 8

Given:

vi = 22.4 m/s

vf = 0 m/s

t = 2.55 s

Find:

d = ??

d = (vi + vf)/2 *t

d = (22.4 m/s + 0 m/s)/2 *2.55 s

d = (11.2 m/s)*2.55 s

d = 28.6 m

Return to Problem 9

Given:

a = -9.8 m/s2

vf = 0 m/s

d = 2.62 m

Find:

vi = ??

vf2 = vi2 + 2*a*d

(0 m/s)2 = vi2 + 2*(-9.8 m/s2)*(2.62 m)

0 m2/s2 = vi2 - 51.35 m2/s2

51.35 m2/s2 = vi2

vi = 7.17 m/s

Answer 2

kangaroo is capable of jumping to a height of 2.62 m

It means it will reach maximum height of 2.62 m when it will jump off with some maximum capable speed from the ground

So here as it will reach to its maximum height the final speed of the kangaroo will be zero

and also we know that during the motion of kangaroo the acceleration of kangaroo is due to gravity which is given by g = 9.8 m/s^2

now we can use kinematics equation to find out take off speed

`v_f^2 - v_i^2 = 2 a d`

here we know that

`v_f = 0`

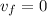
a = - 9.8 m/s^2

d = 2.62 m

now we will have

`0^2 - v_i^2 = 2 * (-9.8)* 2.62`

`- v_i^2 = - -51.352`

`v_i = √(51.352)`

`v_i = 7.17 m/s`

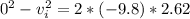
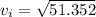
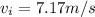
so the take off speed of the kangaroo will be 7.17 m/s and correct answer is "option d"