Question

Help please with this, ASAP!

Answer 1

`a_(n)=12n-8`

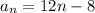
Explanation:

We have been given a recurrence relation
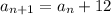`a_(n+1)=a_(n)+12` and the first term of the sequence
`a_(1)=4`.

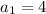We can rewrite the given recurrence relation as:
`a_(n+1)-a_(n)=12`

We know that if difference between two consecutive terms is always constant, the sequence is called an arithmetic sequence. So we are dealing with an arithmetic sequence with first term as 4 and common difference as 12.

We can therefore, write an explicit formula for nth terms of the sequence as.

`a_(n)=a_(1)+(n-1)d\\a_(n)=4+(n-1)(12)\\a_(n)=4+12n-12\\a_(n)=12n-8\\`

This is the required explicit function rule for the given sequence.