Question

Determine the ordered pair that satisfies the equation, 6x - 3y = 5.

a-(9 ,16/3)
b- (6 , -3)
c- (1,−11/3)
d- (-2 ,−17/3)

Answer 1

Option d

Explanation:

Given is a linear equation in x and y as

`6x-3y =5`

To check whether a point satisfies the equation, let us substitute and check whether the equation holds good

a)
`6(9)-3(16/3) = 38 \\eq 5`

b)
`6(6)-3(-3) \\eq 5`

c)
`6(1)-3(-11/3) = 17\\eq 5`

d)
`6(-2)-3(-17/3) = -12+17 =5`

Since last point satisfies the equation, option d is the answer.

Answer 2

Given the equation
`6x-3y=5.`

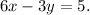
Check all options:

A.
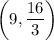`\left(9,(16)/(3)\right)`, this means that
`x=9, y=(16)/(3).` Substitute these numbers into the left side of the equation equation:

`6\cdot 9-3\cdot (16)/(3)=54-16=38\\eq 5.`

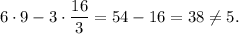
This option is false.

B.
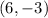`\left(6,-3\right)`, this means that
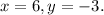`x=6, y=-3.` Substitute these numbers into the left side of the equation equation:

`6\cdot 6-3\cdot (-3)=36+9=45\\eq 5.`

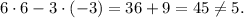
This option is false.

C.
`\left(1,-(11)/(3)\right)`, this means that
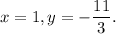`x=1, y=-(11)/(3).` Substitute these numbers into the left side of the equation equation:

`6\cdot 1-3\cdot \left(-(11)/(3)\right)=6+11=17\\eq 5.`

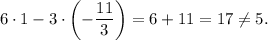
This option is false.

D.
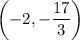`\left(-2,-(17)/(3)\right)`, this means that
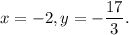`x=-2, y=-(17)/(3).` Substitute these numbers into the left side of the equation equation:

`6\cdot (-2)-3\cdot \left(-(17)/(3)\right)=-12+17=5.`

This option is true.

Answer: correct choice is D.