Question

Please help me with this physics prooblem

Answer 1

Take the missile's starting position to be the origin. Assuming the angles given are taken to be counterclockwise from the positive horizontal axis, the missile has position vector with components

`x=v_0\cos20.0^\circ t+\frac12a_xt^2`

`y=v_0\sin20.0^\circ t+\frac12a_yt^2`

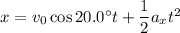
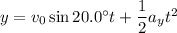
The missile's final position after 9.20 s has to be a vector whose distance from the origin is 19,500 m and situated 32.0 deg relative the positive horizontal axis. This means the final position should have components

`x_(9.20\,\mathrm s)=(19,500\,\mathrm m)\cos32.0^\circ`

`y_(9.20\,\mathrm s)=(19,500\,\mathrm m)\sin32.0^\circ`

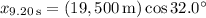
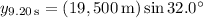
So we have enough information to solve for the components of the acceleration vector,
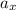`a_x` and
`a_y`:

`x_(9.20\,\mathrm s)=\left(1810\,(\mathrm m)/(\mathrm s)\right)\cos20.0^\circ(9.20\,\mathrm s)+\frac12a_x(9.20\,\mathrm s)^2\implies a_x=21.0\,(\mathrm m)/(\mathrm s^2)`

`y_(9.20\,\mathrm s)=\left(1810\,(\mathrm m)/(\mathrm s)\right)\sin20.0^\circ(9.20\,\mathrm s)+\frac12a_y(9.20\,\mathrm s)^2\implies a_y=110\,(\mathrm m)/(\mathrm s^2)`

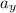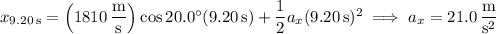
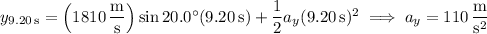
The acceleration vector then has direction
`\theta` where

`\tan\theta=(a_y)/(a_x)\implies\theta=79.2^\circ`