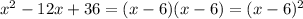Answer:
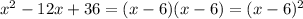
Explanation:
We are given the following expression:
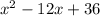
We need to factor the given expression.
We will do this with the help of technique of splitting the middle term.
Factorization can be done as:

Thus, the factored form of given expression is: