1 Answer

Fiatjaf · Answer 1 · 2019-08-10T08:18:19+0000

Answer-

The abs. minimum value of the given function was found to be 3.

Solution-

Here, the given function is,

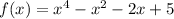
f(x)=x^4-x^2-2x+5

Then, calculating its first derivative,

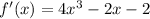
${f}'(x)=4x^3-2x-2$

Then, calculating its second derivative,

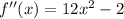
${f}''(x)=12x^2-2$

Then, calculating all the critical values of the given function by equating the first derivative to 0,

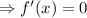
$\Rightarrow {f}'(x)=0$

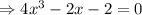
$\Rightarrow 4x^3-2x-2=0$

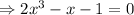
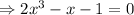
$\Rightarrow 2x^3-x-1=0$

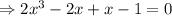
$\Rightarrow 2x^3-2x+x-1=0$

$\Rightarrow 2x(x^2-1)+(x-1)=0$

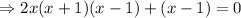
$\Rightarrow 2x(x+1)(x-1)+(x-1)=0$

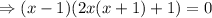
$\Rightarrow (x-1)(2x(x+1)+1)=0$

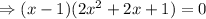
$\Rightarrow (x-1)(2x^2+2x+1)=0$

$\Rightarrow (x-1)=0$ ( ∵ ignoring the imaginary roots)

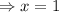
$\Rightarrow x=1$

Putting the value of x, in the second derivative,

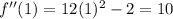
${f}''(1)=12(1)^2-2=10$

As, the value of f"(x) is positive, the function attains its minimum value at x=1.

So, f(1) will give the absolute minimum value of the function,

f(1)=(1)^4-(1)^2-2(1)+5=3

∴ The abs. minimum value of the given function is 3.

Please log in or register to add a comment.