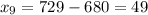Question

I need help with these two problems. Need an explanation, steps, and an answer.

Answer 1

Let
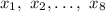`x_1,\ x_2,\ldots,\ x_8` be the scores of the first 8 quizzes. We know that the average of these scores is 85, so we have

`(x_1+x_2+\ldots+x_8)/(8) = 85 \iff x_1+x_2+\ldots+x_8 = 85 \cdot 8 = 680`

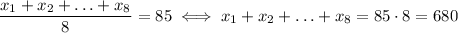
The average of the first 9 scores is 81, and it is given by

`(x_1+x_2+\ldots+x_8+x_9)/(9) = 81`

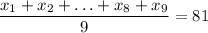
But we know that the sum of the first 8 is 680:

`(680+x_9)/(9) = 81`

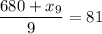
And we can solve for the nineth score: multiply both sides by 9:

`680+x_9 = 729`

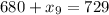
Subtract 680 from both sides:

`x_9 = 729 - 680 = 49`