Question

The sides of a ladder are parallel. Since the rungs are perpendicular to one side of the ladder, what conclusion can be made?

- The sides are parallel to the rungs.


- The rungs are parallel to the sides.


- The sides are perpendicular to each other.


- The rungs are perpendicular to the other side.

Answer 1

- The rungs are perpendicular to the other side.

Answer 2

The rungs are perpendicular to the other side.

Explanation:

Given

The sides of ladder are parallel.Rungs is perpendicular to one side of the ladder.

Let
`a\parallel b`

`a\perp c`

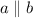
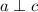
When two lines are parallel then the slopes of two lines are equal.

We can say
`m_1=m_2`

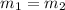
Where
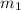`m_1`= slope of line a( side of ladder)

`m_2`= solpe of line b( side of ladder)

When two lines are perpendicular then slopes of two lines are opposite reciprocal to each other.

We can say
`m_2=-(1)/(m_3)`

Where
`m_2`= Slope of line b

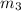`m_3`=Slope of line c (rung)

By transitive property of equality we get

`m_1=-(1)/(m_3)`

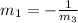
Hence, the slope of side of ladder a and rung c are opposite reciprocal to each other.Therefore , the rungs are perpendicular to the other side.