Question

Factor the expression completely over the complex numbers.

x3−4x2+4x−16



Enter your answer in the box.

Answer 1

(x-4) (x-2i) (x+2i)

Explanation:

x^3−4x^2+4x−16

I will factor by grouping

x^3−4x^2+ 4x−16

The first group is the first 2 terms. I can factor out an x^2

x^2 (x-4) + 4x-16

The second group I can factor out a 4

x^2 (x-4) + 4(x-4)

Now I can factor out (x-4)

(x-4) (x^2 +4)

We know that x^2 + 4 factors into +2i and -2i because

(a^2 -b^2) = (a-b) (a+b) but we have (a^2 + b^2) = (a-bi) (a+bi)

(x-4) (x-2i) (x+2i)

Answer 2

The factor form of given expression is (x-4)(x-2i)(x+2i).

Explanation:

The given expression is

`x^3-4x^2+4x-16`

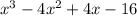
It can be written as

`f(x)=x^3-4x^2+4x-16`

According to the rational root theorem, all possible rational roots are in the form of

`(a_0)/(a_n)`

Where, a₀ is constant term and
`a_n` is leading coefficient.

`f(4)=4^3-4(4)^2+4(4)-16=0`

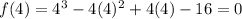
Since the value of f(x) is 0 at x=4, therefore 4 is a root of the function and (x-4) is a factor of given expression.

Use synthetic method to find the remaining factors.

`(x^3-4x^2+4x-16)=(x-4)(x^2+4)`

`(x^3-4x^2+4x-16)=(x-4)(x^2-(2i)^2)`

`(x^3-4x^2+4x-16)=(x-4)(x-2i)(x+2i)`

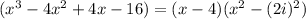
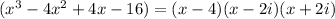
Therefore the factor form of given expression is (x-4)(x-2i)(x+2i).