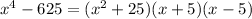You have to observe that
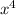 and 625 are both squares (of
and 625 are both squares (of
 and 25, respectively). So, you can use the "difference of square" pattern for factorization:
and 25, respectively). So, you can use the "difference of square" pattern for factorization:
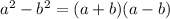
to write
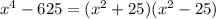
Note that, again,
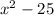 is a difference of square:
is a difference of square:
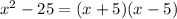
On the other hands,
 admits no factorization, because it's a second-degree polynomial (thus a parabola) with no solutions.
admits no factorization, because it's a second-degree polynomial (thus a parabola) with no solutions.
So, the whole expression becomes