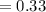Question

A group of 10 students participate in chess club, karate club, or neither.

Let event A = The student is in chess club.
Let event B = The student is in karate club.
One of these students is randomly selected. What is P(A|B)?

A. 2/6 ≈ 0.33
B. 4/6 ≈ 0.67
C. 6/10 ≈ 0.60
D. 2/10 ≈ 0.20

If you can, please explain how you got your answer. I would like to know how you solved it.

Answer 1

Answer: 2/6 ~ 0.33

Step-by-step explanation: took quiz

Answer 2

Total number of students = 10

As we have to find

P(A/B) = Probability( A when B has happend)

P(A/B)= P(A intersection B)/P(B)

According to given figure only yolanda and Rob are in both club

Therefore,P(A intersection B)
`=(2)/(10)`

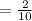
Number of student in karate club =6

P(B)
`= (6)/(10)`

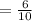
P(A/B)
`= (2)/(10)/{(6)/(10)`

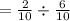
Converting division into multiplication by reciprocating the term after division

P(A/B)
`= (2)/(10)*{(10)/(6)`

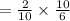
On solving we get ,

P(A/B)
`= (2)/(6)`

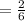
P(A/B)
`=(1)/(3)`

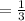
P(A/B)
`=0.33`