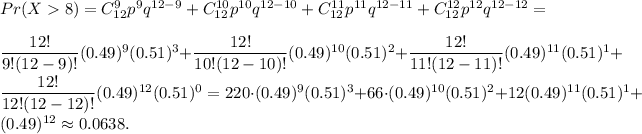Question

(CO 4) Forty-nine percent of US teens have heard of a fax machine. You randomly select 12 US teens. Find the probability that the number of these selected teens that have heard of a fax machine is exactly six (first answer listed below). Find the probability that the number is more than 8 (second answer listed below).

Answer 1

Forty-nine percent of US teens have heard of a fax machine, then the probability that the teen has heard of a tax machine is p=0.49 and the probability that the tenn hasn't heard of a tax machine is q=1-p=1-0.49=0.51.

Use binomial distribution.

The probability that among 12 randomly selected teens exactly 6 have heard of a fax machine is

`Pr(X=6)=C_(12)^6p^6q^(12-6)=(12!)/(6!(12-6)!)(0.49)^6(0.51)^6=\\\\(6!\cdot 7\cdot 8\cdot 9\cdot 10\cdot 11\cdot 12)/(6!\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6)(0.49\cdot 0.51)^6=924\cdot (0.2499)^6\approx 0.22505.`

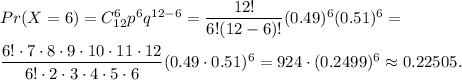
The probability that among 12 randomly selected teens more than 8 have heard of a fax machine is

`Pr(X>8)=C_(12)^9p^9q^(12-9)+C_(12)^(10)p^(10)q^(12-10)+C_(12)^(11)p^(11)q^(12-11)+C_(12)^(12)p^(12)q^(12-12)=\\\\(12!)/(9!(12-9)!)(0.49)^9(0.51)^3+(12!)/(10!(12-10)!)(0.49)^(10)(0.51)^2+(12!)/(11!(12-11)!)(0.49)^(11)(0.51)^1+(12!)/(12!(12-12)!)(0.49)^(12)(0.51)^0=220\cdot (0.49)^9(0.51)^3+66\cdot (0.49)^(10)(0.51)^2+12(0.49)^(11)(0.51)^1+(0.49)^(12)\approx 0.0638.`