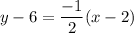Answer with explanation:
Part--1:
We know that a equation in point-slope form is represented by:

where m is the slope of the line and
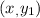 is a point through which the line passes.
is a point through which the line passes.
Consider a equation in a point-slope form as:
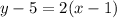
This means that the slope of the line is: 5
and the line passes through the point (1,5).
Part--2:
Now as we know that if a line has a slope as m then the perpendicular line has a slope: -1/m
Since,

Let this perpendicular line passes through (2,6)
Hence, the equation of a line in point slope form is given by: