(a) Let x be the cost of one of Brian's items, then cost of all 4 items bought by Brian will be 4x.
We have been given that Chris bought 3 items that each cost $2.50 more than Brian’s items each cost. The price of each item bought by Chris will be x+2.5. Therefore, the cost of all 3 items bought by Chris will be
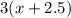 .
.
(b) We are told that Brian and Chris both paid the same amount of money, so we can equate costs of Brian's 4 items and Chris's 3 items as:
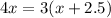
Now let us solve for x by distributing 3.
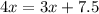
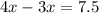
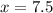
Therefore, cost of Brian's each item is $7.5.
Now let us find price of Chris's each item.
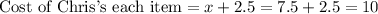
Therefore, cost of Chris's each item is $10.
(c) Now let us check our solution by substituting x=7.5 in
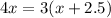 .
.


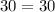
We can see that both Brian and Chris spent equal amount of money that is $30, therefore, our solution is correct.