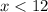Question

Select all the possible solutions for 2x +7 < 3x-5

Answer 1

We have to find all the possible solutions for the inequality
`2x+7<3x-5`.

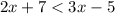The given inequality can be solved as,

Subtracting 7 from both side , we get

`2x+7-7 < 3x-5-7\\\\\Rightarrow 2x<3x-12`

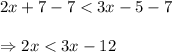
Now, Subtracting 3x from both side, we get

`2x-3x<3x-12-3x\\\Rightarrow -x <-12\\`

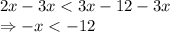
As we here we can see that both sides have similar sign, so we can cancel them out.

`\Rightarrow x < 12`

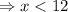
Hence, the possible solution of the inequality
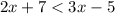`2x+7<3x-5` is
`x< 12`