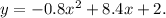Question

The value of a particular rookie baseball card was $2.00 when it was first printed. Five years later, when the player was at his peak, the card was valued at $25.00. Ten years after printing, the card was valued at $8.00.

Model the above scenario, showing the value of the card, y, with respect to years since it was printed, x. Write the equation in standard form, y = ax2 + bx + c, where a, b, and c are real numbers rounded to the nearest tenth.

Answer 1

thirty four

`25 + 2 + 8`

Answer 2

Let t be the time passed in years and y be the value of baseball card.

You know that

• when x=0, then y=2;
• when x=5, then y=25;
• when x=10, y=8.

The equation in standard form is
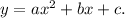`y=ax^2+bx+c.` Substitute given data into the equation:

`a\cdot 0^2+b\cdot 0+c=2,\\\\a\cdot 5^2+b\cdot 5+c=25,\\\\a\cdot 10^2+b\cdot 10+c=8.`

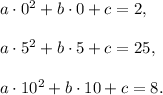
Solve the system of equations:

`\left\{\begin{array}{l}c=2\\25a+5b+c=25\\100a+10b+c=8\end{array}\right.\Rightarrow \left\{\begin{array}{l}c=2\\25a+5b=23\\100a+10b=6\end{array}\right.\Rightarrow`

`\left\{\begin{array}{l}c=2\\a=-0.76\approx -0.8\\b=8.4\end{array}\right.`

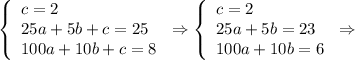
Then the parabola equation is

`y=-0.8x^2+8.4x+2.`