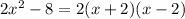Question

Factor the polynomial completely

Answer 1

We have
`2x^2-8`.

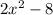First let us factor the 2 to obtain,

`2(x^2-4)`

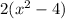
We can now see clearly that the expression inside the parentheses is a difference of two squares.

We now write the 4 as 2². So that we obtain the expression,

`2(x^2-2^2)`

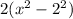
Recall that

`a^2-b^2=(a+b)(a-b)`

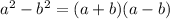
Hence our expression becomes,

`2(x+2)(x-2)`

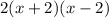
Therefore, when factored completely,

`2x^2-8=2(x+2)(x-2)`