(A) The resistance of the block of aluminum is given by:
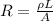
where
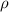 is the aluminum resistivity
is the aluminum resistivity
L is the length of the cylinder
A is the cross-sectional area of the cylinder
We already know the aluminum resistivity (
 ) and the length of the cylinder (L=20 m), so we must find the cross-sectional area A, which is given by the difference between the area of the larger cylinder and the area of the radial hole:
) and the length of the cylinder (L=20 m), so we must find the cross-sectional area A, which is given by the difference between the area of the larger cylinder and the area of the radial hole:
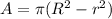
where
 and
and
 (assuming that the 20 mm removed radially refers to the radius of the hole).
(assuming that the 20 mm removed radially refers to the radius of the hole).
Therefore, the cross-sectional area is
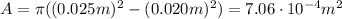
Substituting into the initial formula of the resistance, we find:
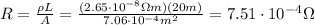
(B) The resistivity of the tungsten is
 , so a cylinder of tungsten of the same size would have a resistance of
, so a cylinder of tungsten of the same size would have a resistance of
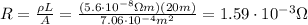
The behaviour of the resistance versus temperature is given by:
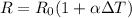
where
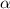 is a coefficient that for aluminum is equal to
is a coefficient that for aluminum is equal to
 , R0 is the resistance of the piece of aluminum we found at point (A), and R is the resistance of the tungsten. Re-arranging the formula and substituting, we find
, R0 is the resistance of the piece of aluminum we found at point (A), and R is the resistance of the tungsten. Re-arranging the formula and substituting, we find

So, the temperature must increase by 259.3 degrees.
(C) The power dissipated is given by:
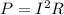
where I=30 A is the current. Substituting the numbers into the formula, we find
