Answer: (i) The unit rate at which online jewelry sales have been increasing is 1.33 billion dollars per year.
(ii) The online jewelry sales in 2019 will be 191.7 billion dollars.
Explanation:
In 2003, sales were approximately 2 billion dollars and in 2010, they were approximately 14.8 billion dollars.
(i) If
 is the number of years after 2003 and
is the number of years after 2003 and
 is the amount of sales....
is the amount of sales....
then the equation will be:
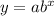 , where
, where
 is the initial amount and
is the initial amount and
 is the growth rate.
is the growth rate.
for 2003,
 and for 2010,
and for 2010,
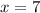
So, the two points in form of (x, y) will be:
 and
and

Now plugging these two points int the above equation....
![2= ab^0\\ \\ a= 2\\ \\ and\\ \\ 14.8=ab^7\\ \\ 14.8=2*b^7\\ \\ b^7=7.4\\ \\b= \sqrt[7]{7.4}=1.3309.... \approx 1.33](https://img.qammunity.org/2019/formulas/mathematics/college/bz0ruyld0f7qx5e3vbtd6qraujmczaefp3.png)
Thus, the online jewelry sales have been increasing at a rate of 1.33 billion dollars per year.
(ii) As we got
 and
and
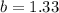 , so the equation will be now:
, so the equation will be now:
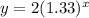
For the year 2019, the value of
 will be: (2019-2003) = 16
will be: (2019-2003) = 16
So plugging
 into the above equation, we will get.....
into the above equation, we will get.....
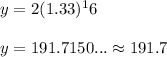
(Rounded to the nearest tenth)
Thus, the online jewelry sales in 2019 will be 191.7 billion dollars.