Question

How do you do this!?!

11x + y = 4, x + y = -2, x - 2y = 18

How can you determine which equations can be graphed more easily using x- and y-intercepts, rewriting in slope-intercept form, or using a table of values?

Which method works best for you personally? When does it not work as well?

Answer 1

11x + y = 4

x | y

0 | 4

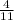`(4)/(11)` | 0

plot the y-intercept (0, 4) and the x-intercept (
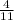`(4)/(11)`, 0)

or

11x + y = 4

-11x -11x

y = -11x + 4 ⇒ m =
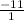`(-11)/(1)`, b = 4

plot at point the y-intercept "b = 4" (0,4). plot the next point using the slope "m =
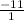`(-11)/(1)`" from point (0,4), count down 11 and to the right 1 (1,-7).

Using intercepts would not provide an accurate graph because you have to estimte where (
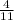`(4)/(11)`, 0) is, so it is best to use slope-intercept form.

***********************************************************************************************************

x + y = -2

x | y

0 | -2

-2 | 0

plot the y-intercept (0, -2) and the x-intercept (-2, 0)

or

x + y = -2

-x -x

y = -x - 2 ⇒ m =
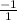`(-1)/(1)`, b = -2

plot at point the y-intercept "b = -2" (0,-2). plot the next point using the slope "m =
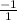`(-1)/(1)`" from point (0,-2), count down 1 and to the right 1 (1,-3).

Both methods are easy to use so either can be used.

**********************************************************************************************************

x - 2y = 18

x | y

0 | -9

18 | 0

plot the y-intercept (0, -9) and the x-intercept (18, 0)

or

x - 2y = 18

-x -x

-2y = -x + 18

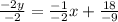
`(-2y)/(-2) = (-1)/(-2)x + (18)/(-9)`

y =
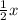`(1)/(2)x` - 9

plot at point the y-intercept "b = -9" (0,-9). plot the next point using the slope "m =
`(1)/(2)`" from point (0,-9), count up 1 and to the right 2 (2,-8).

Using intercepts will make a large graph since you have to plot (18,0) so it is best to use the slope-intercept form.