we can see that
zeros are at x=-3 , x=2 , x=3
now, we can set up function
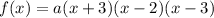
now, we can select any one point and then we can find 'a'
(0,36)
x=0 and f(x)=36
we can plug it and then we can find 'a'


now, we can plug it back
and we get

now, we can multiply it
we get
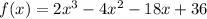 ............Answer
............Answer