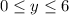Answer:

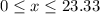
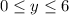
Explanation:
The machine always takes 10 minutes (or 1/6 hours) to warm up and performs each cycle in 15 minutes, or 0.25 hours.
The maximum amount of daily hours that the machine can work is 6 hours.
Therefore we can represent this situation by means of an equation of the form:

Where
y = daily amount of hours the machine works.
x = number of daily cycles performed.
This equation is a linear function. Because it has the form y = ax where a is a real number
The graph of this equation is shown in the attached image, where the gray shaded area represents the domain of the function.
The domain of the function is:
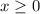 (because you can not perform less than zero cycles a day)
(because you can not perform less than zero cycles a day)
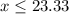 . Because the machine can not exceed 6 hours per day, then it can not do more than 23.33 cycles.
. Because the machine can not exceed 6 hours per day, then it can not do more than 23.33 cycles.
So:
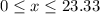
The range of the function is:
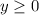 (because you can not work less than 0 hours a day)
(because you can not work less than 0 hours a day)
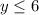 (because the machine can not work more than 6 hours a day)
(because the machine can not work more than 6 hours a day)
So